AHC024解法紹介 〜曲率の離散類似による連結判定〜
問題
コンテスト中の方針
以下の焼きなまし(もどき)
- 近傍
- 1点を隣の色で塗る
- 十字で2マス同時に動かす
- 評価関数:生スコアを使い、以下の値でタイブレークを行う*1
- 境界線の長さの和
- 境界線が短い方が全体的にきれいなので小さくしやすそう
- 各タイルのサイズの2乗和
- 中央のタイルが大きいままになりがちなので、タイルの大きさを均したい
- 境界線の長さの和
- 温度:スコアが悪化しても確率p=50.0%で受理する。25,000回のイテレーションごとにpを0.1%小さくする*2
曲率の離散類似による連結判定
上の方針の実装で主に問題となるのは各タイルの連結性の判定である。wataさんの解説では周囲の3x3だけを見て簡易的に判定しており、shun_PIさんの延長戦解法では5x5を見ることでさらにスコアをあげている:
しゅんぴー(Shun_PI) on X: "関節点判定を5*5にしたら100点上がった(24ビットメモ化)" / X
ここでは、別の判定方法を紹介する。以下の値をそれぞれの頂点の周りでカウントして和をとることで概ね連結性に対応する値が得られる。(1点更新ではその周りの4頂点についてのみこの値を計算し直せば良い、実際には周囲の3x3マスの情報をキーとして差分を前計算できる)
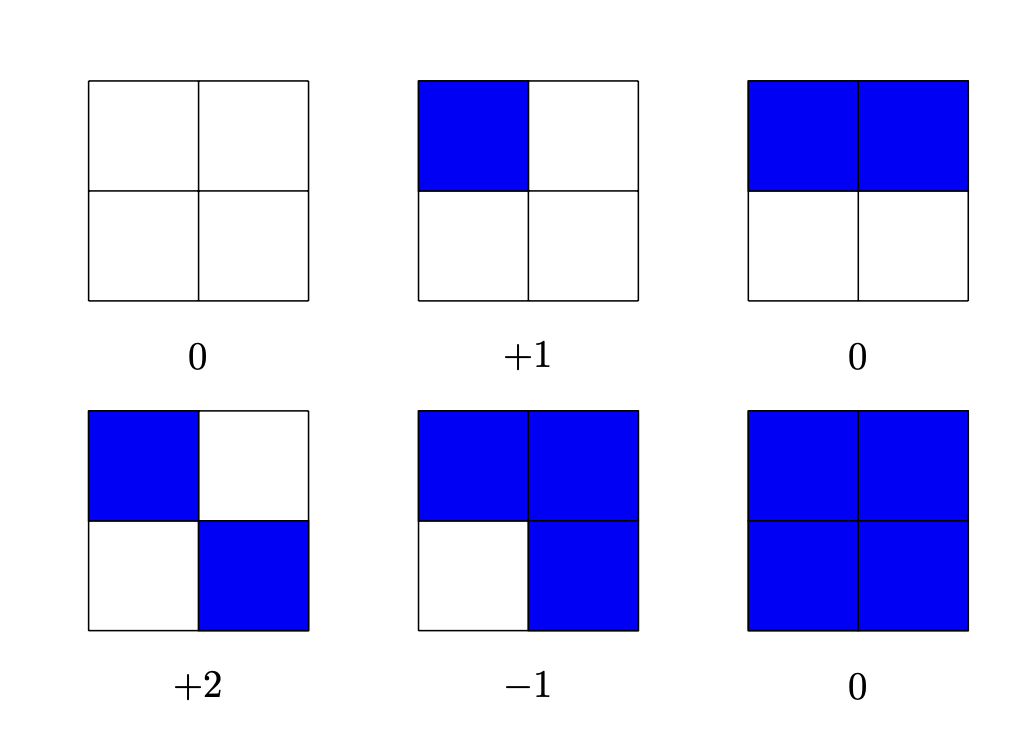
イメージとしてはタイルの縁を反時計回りになぞったときに左に何回曲がったかを数えており、オイラー標数に対応する。タイルに空いている穴の数が変わらない限りこの値を連結性の判定に用いることができ、今回はタイル間の接続判定が保存されるので穴の数は変わらない。というのは間違いで、以下の図右のようなものを穴と認識できないので以下の遷移をrejectしてしまう。

今回の入力ではそれぞれのタイルの穴の数は少ない(多分たかだか2つくらい?)ので、個別に対処すれば局所的な更新だけで連結性判定が完全にできるはず
他の上位解法のまとめ
上位解法というか、AHC024についての言及で気になったものをまとめました。
#AHC024
— eijirou (@eijirou_kyopro) 2023年9月27日
延長戦337,025点
- 遷移は1or2マスの変更
- 生スコアを局所改善
-「普通の焼きなまし」を「高温と低温を繰り返す焼きなまし」にしたら300点ぐらい上がった(山登り+kickのほうがいいかも)
- 二点スタートで少しよくなった
- 行・列の削除を入れてもよくならなかった
あまり上手く理由づけできないが、スコアが離散的すぎて焼きなましの終盤で登り切らないとその周辺の解の良さがわかりづらい、みたいなことかもしれない
- dfsで有効なn点changeを求める
— _____ (@rho__o) 2023年9月27日
- 無駄なランダムウォークを防ぐために新たに有効になった近傍をsetに突っ込んで次の近傍はそのsetから取り出す
などを実装すると337,683が出るらしいです
n点changeは15M回くらい試せている(失敗確率は75%くらい)
詳細はよくわかってないが、延長戦1位解法なのですごい。ランダムウォークが無駄かどうかを事前に把握することは本当に可能なのかな・・・
外出中ふと思ったのですが、AHC024の1~2点変更する遷移って基本十字型を回転させることはできないから、左の解から右の解に到達できなかったりしませんか?
— MON.T+α (@montplusa) 2023年9月27日
(このポイントがスコアにおいて致命的になるかはともかくとして・・・) pic.twitter.com/dN46LsF51w
延長戦をした感じでは、焼きなましの試行回数が十分でないとこの近傍を加えてもあんまりスコア増えなかったけど、ある程度高速化して試行回数が増えるとそれなりに効果ありそう
延長戦解法
以下の焼きなまし
- 近傍
- 1点を隣の色で塗る
- 十字で2マス同時に動かす、連鎖させる
- 十字の回転
- 評価関数:生スコア
- 温度:普通の焼きなまし
連結性の判定は上で解説した方針で穴が1つの場合だけ(正確には、穴あきのタイルそれぞれについて単色の穴を1つまで)個別に対応するようにした。
また、実装をしなおして、諸々高速化した。受理される率が低かったので、隣接する2マスで色が異なるものの集合を管理するようにしたらスコアがかなり改善した。
40M~50Mくらい試行して、受理されるのは4Mくらい
再延長戦
実は最近ALGO ARTISでアルバイトを始めました。(今のところAHCの復習しかしてません / この記事も部分的にはsupported by AAです)この記事の内容を社内で発表したところ、時間短くして複数回実行みたいにした方が良いのでは?というアドバイスをいただいて、そのように書き直したら100点くらい上がりました。
TLギリギリまで使ったりいらないデバッグ出力消したりしたら延長戦1位まで46点差まで迫りましたが、少し届きませんでした。熱烈高速化すれば抜けるくらいの差だと思いますが、1位の点数も高速化で伸ばす余地はあるはずなのでここでやめておきます・・・
コンパイラ変えたら少し速くなるよと教えていただいてClangのC++23にしたら25点上がりました。ここでやめておきます・・・